Model-Dependent Transformations

What are model dependent transformations?

A model-dependent transformation is a transformation of a feature that is specific to one model, and is consistently applied in training and inference pipelines. It is typically an encoding of the feature value that uses the training dataset as the reference window when computing the encoding. There is a direct benefit of having model-dependent transformations decoupled from model-independent transformations in that it allows for flexibility in feature engineering, making it easier to adapt and optimize features for different models without affecting the underlying raw data.

Why are model dependent transformations important?

Model-dependent transformations (feature encoding) are needed for 

1. data compatibility or 
2. to improve model performance. 

For data compatibility, your modeling algorithm may need, for example, to convert non-numeric features into numerical values or to resize inputs to a fixed size.

For improved model performance, depending on your modeling algorithm, you may need to re-scale a numerical feature into smaller bound (e.g, [0,1] in the figure above) or standardize the distribution of a numerical feature with a Gaussian-like distribution so that it has a mean of ‘0’ and a standard-deviation of ‘1’ or you may also need to tokenize or lower-case text features.

An important point to note is that model-dependent transformations nearly always require a snapshot of data to be computed (i.e., the training data set). So, a min-max scalar requires the min/max values in the snapshot. Normalization requires the mean and standard deviation in the snapshot. A categorical encoder uses all the categories in the snapshot. 

What are examples of model-dependent transformations?

The following are examples of model-dependent transformations. They are parameterized by properties of the snapshot (e.g., mean std-dev, min, max, set of categories) and the type of modeling algorithm used:

• Encoding: transform a categorical variable (e.g., a string) into a numerical representation;
• Normalization: scales feature values to make the data homogenous - used by algorithms when the data distribution is unknown or the data doesn't have to follow a Gaussian Distribution;
• Standardization: rescale the features so that their mean is 0 and standard deviation becomes 1 - used by algorithms that make assumptions about the data distribution, such as logistic regression and some ANNs that assume a Gaussian distribution;
• Imputation: if you are using a reference window to impute a feature value (e.g., mean).

It is not uncommon when building ML models to apply various algorithms on raw, normalized, and standardized data to find the best algorithm for your available data.

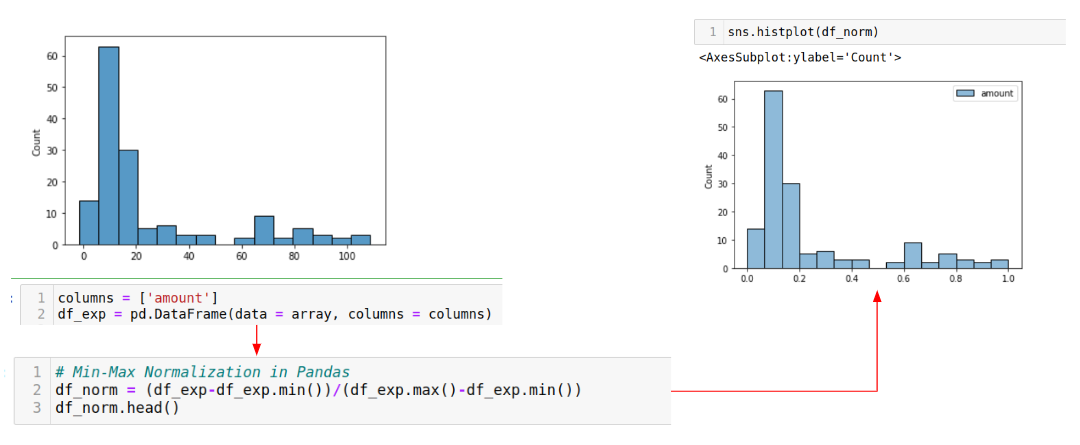
When you plot the data distribution of a feature, you can see if you need to transform it before using it in your model. Here, we apply min-max scaling in Pandas to the numerical feature ‘amount’. Notice that the x-axis is scaled from 0-110 (LHS) down to 0.0-1.0 (RHS).

Here is a short Python snippet showing how to standardize all of the features in a train set:

 from sklearn.preprocessing import StandardScaler

# create an instance of the StandardScaler object
scaler = StandardScaler()

# assume X_train is your train set features with numerical data
X_train, X_test, y_train, y_test = \
feature_view.train_test_split (test_ratio=0.2)
# fit the scaler to your data
scaler.fit(X_train)

# apply the scaler to transform your data
X_train_normalized = scaler.transform(X_train)

This example demonstrates how to standardize numerical data by applying the standard scalar preprocessing function from Scikit-Learn - for each feature value, it subtracts the mean and scales to unit variance:

z = (x - u) / s

Where u is the mean of the train set samples, and s is the standard deviation of the train set samples.